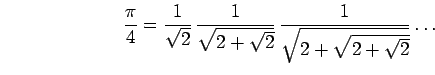 ou
ou  ) qui est la bijection réciproque de
l'application tangente. Il suffit donc de calculer
) qui est la bijection réciproque de
l'application tangente. Il suffit donc de calculer
L'arctangente (notée 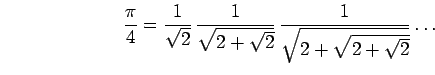 ou
ou  ) qui est la bijection réciproque de
l'application tangente. Il suffit donc de calculer
) qui est la bijection réciproque de
l'application tangente. Il suffit donc de calculer
![]() .
.
La dérivée est définiee par
![]() . En intégrant
le développement limité d'
. En intégrant
le développement limité d'![]() ,
Gregory découvre la
,
Gregory découvre la
![]()
Leibniz (1646-1716) obtient la même formule au même moment, et c'est en fait lui qui va la publier en 1674.