


Next: Remarque. Up: Problème (dit) de Napoléon.
Previous: Problème: Contents
Cette construction, en six étapes, est celle de
Napoléon et Mascheroni.
- D'un point
 du cercle , un arc de cercle de
rayon quelconque qui recoupe le cercle en
du cercle , un arc de cercle de
rayon quelconque qui recoupe le cercle en 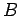 et
et

- arc de cercle de centre
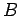 et de rayon
et de rayon
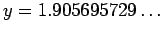
- arc de cercle de centre
 et de rayon
et de rayon
 . Ces deux arcs se coupent en
. Ces deux arcs se coupent en  .
.
- arc de cercle de centre
 et de rayon
et de rayon
 qui recoupe le premier arc (de
l'étape 1.) en
qui recoupe le premier arc (de
l'étape 1.) en  et
et  .
.
- arc de cercle de centre
 et de rayon
et de rayon

- arc de cercle de centre
 et rayon
et rayon
 . ces deux arcs se coupent en
. ces deux arcs se coupent en 
Il ne reste plus qu'à prouver que  est
bien le centre du cercle... Ce qui n'est pas très difficile.
Ce classique vient du dictionnaire des
Mathématiques[].
est
bien le centre du cercle... Ce qui n'est pas très difficile.
Ce classique vient du dictionnaire des
Mathématiques[].
Faq de fr.sci.maths 2003-12-14
![]() est
bien le centre du cercle... Ce qui n'est pas très difficile.
Ce classique vient du dictionnaire des
Mathématiques[].
est
bien le centre du cercle... Ce qui n'est pas très difficile.
Ce classique vient du dictionnaire des
Mathématiques[].