Solution.

On appelle:

• BF l'échelle qui va du haut à gauche au bas à droite (B en haut à gauche) ;
• EA l'échelle qui va du bas à gauche au haut à droite (E en bas)
• I le point d'intersection des deux échelles,
• H la projection orthogonale de I sur le sol.

On pose:

$$\begin{array}{cccccccccccc} AF & = & x & ; & EF & = & y & ;... ...E & = & a & ; & BF & = & b & ; & IH & = & c & ; \ \end{array}$$

On applique le théorème de Pythagore dans le triangle FAE rectangle en F. $AF^2 + EF^2 = AE^2$. C'est-à-dire: $x^2 + y^2 = a^2$.

On applique le théorème de Pythagore dans le triangle FEB rectangle en E. $EF^2 + BE^2 = BF^2$. C'est-à-dire: $y^2 + z^2 = b^2$.

On applique le théorème de Thalès avec les parallèles (BE), (IH) et (AF). $\frac{c}{x} + \frac{c}{z} = \frac{EH}{EF} + \frac{HF}{EF} = \frac{EH + HF}{EF} = 1$ , d'où $\frac{c}{z} = \frac{x-c}{x}$

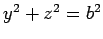
Il vient donc: $x^2 - z^2 = a^2 - b^2$ et $z = c \times \frac{x}{x-c}$ Et puis: $x^2 - (c \frac{x}{x-c})^2 = a^2 - b^2$ ce qui conduit à

$$x^4 - 2 c x^3 - (a^2 - b^2) x^2 +2 c (a^2-b^2) x - c^2 (a^2-b^2)=0$$

Cette équation de degré 4 se résout par radicaux ou de manière approchée avec tout outil de calcul. On a ensuite: $y = \sqrt{a^2 - x^2}$.

On a ici: $a = 14$, $b = 10$, $c = 5$, d'où l'équation:

$$x^4 - 10 x^3 - 96 x^2 + 960 x - 2400 = 0$$

Et donc: $x = 12.78405$ avec un outil de calcul. Puis $y = \sqrt{a^2-x^2} = 5.706842$.