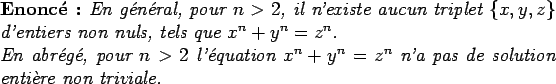 . Le produit
. Le produit
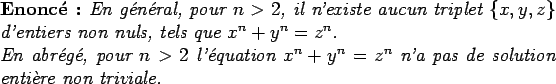 . Cela signifie que
. Cela signifie que
 , ni
, ni  . Notre
liste ne peut donc pas être complète, il existe donc
une infinité de nombres premiers.
. Notre
liste ne peut donc pas être complète, il existe donc
une infinité de nombres premiers.Oui. En voici une démonstration par contradiction. Noter qu'après le Théorème de Pythagore, c'est sûrement le résultat mathématique pour lequel on connaît le plus de démonstrations différentes.
Supposons qu'il n'en existe qu'un nombre fini ![]() ,
qui seraient
,
qui seraient
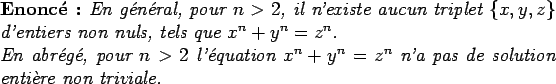 . Le produit
. Le produit
![]() est divisible
par chacun de ces premiers
est divisible
par chacun de ces premiers
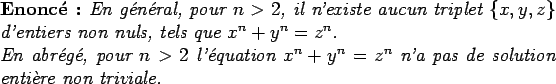 . Cela signifie que
. Cela signifie que
![]() n'est
divisible par aucun d'entre eux. Donc le plus petit diviseur
(excepté
n'est
divisible par aucun d'entre eux. Donc le plus petit diviseur
(excepté ![]() ) de ce nombre, qui est
forcément un nombre premier, n'est ni
) de ce nombre, qui est
forcément un nombre premier, n'est ni  , ni
, ni ![]() , ..., ni
, ..., ni  . Notre
liste ne peut donc pas être complète, il existe donc
une infinité de nombres premiers.
. Notre
liste ne peut donc pas être complète, il existe donc
une infinité de nombres premiers.