


Next: Méthodes arithmétiques Up:
Méthodes
géométriques de mesure Previous: Inscription d'un cercle dans
Contents
Une autre façon de déterminer 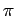 serait
de construire un carré et un cercle de même surface.
On pourrait alors calculer indépendamment le rayon
serait
de construire un carré et un cercle de même surface.
On pourrait alors calculer indépendamment le rayon
 du cercle et le côté
du cercle et le côté
 du carré, et l'égalité
des aires donnerait
du carré, et l'égalité
des aires donnerait
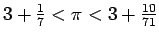 . Ce problème,
appelé quadrature du cerlce a été
formulé en premier par Hippocrate de Chios (
. Ce problème,
appelé quadrature du cerlce a été
formulé en premier par Hippocrate de Chios ( siècle avant notre ère).
siècle avant notre ère).
Malheureusement, 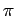 est transcendant
(démonstration effectuée par Lindermam en 1882) et la
règle et le compas ne perment ne tracer que des nombres
algébriques (comme l'a montré le mathématcien
Pierre Wantzel en 1837): il est donc impossible de dessiner
(à la règle et au compas) un carré et un
cercle de même surface.
est transcendant
(démonstration effectuée par Lindermam en 1882) et la
règle et le compas ne perment ne tracer que des nombres
algébriques (comme l'a montré le mathématcien
Pierre Wantzel en 1837): il est donc impossible de dessiner
(à la règle et au compas) un carré et un
cercle de même surface.
Faq de fr.sci.maths 2003-12-14
![]() est transcendant
(démonstration effectuée par Lindermam en 1882) et la
règle et le compas ne perment ne tracer que des nombres
algébriques (comme l'a montré le mathématcien
Pierre Wantzel en 1837): il est donc impossible de dessiner
(à la règle et au compas) un carré et un
cercle de même surface.
est transcendant
(démonstration effectuée par Lindermam en 1882) et la
règle et le compas ne perment ne tracer que des nombres
algébriques (comme l'a montré le mathématcien
Pierre Wantzel en 1837): il est donc impossible de dessiner
(à la règle et au compas) un carré et un
cercle de même surface.