Pour obtenir l'aire ![]() commune aux deux cercles, on
additionne l'aire
commune aux deux cercles, on
additionne l'aire ![]() du secteur
du secteur ![]() du cercle
du cercle ![]() , l'aire
, l'aire ![]() du secteur
du secteur ![]() du cercle
du cercle ![]() ,
et on soustrait l'aire
,
et on soustrait l'aire ![]() du quadrilatère
du quadrilatère
![]() (qui serait comptée deux fois
sinon).
(qui serait comptée deux fois
sinon).
On prend comme inconnue l'angle
![]() en radians. On a:
en radians. On a:
![]() (dans le triangle rectangle
(dans le triangle rectangle
![]() ) d'où
) d'où ![]() . Donc
. Donc
L'équation à résoudre est
![]() ou encore:
ou encore:
Ce qui se simplifie en:
![]() En
posant
En
posant 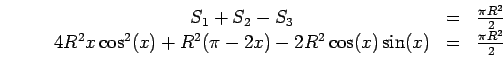 :
:
![]()
![]() est l'angle
est l'angle ![]() et est compris entre
et est compris entre ![]() et
et ![]() . La
fonction
. La
fonction
![]() est continue et
strictement croissante sur
est continue et
strictement croissante sur ![]() et
et
![]() et
et ![]() .
L'équation
.
L'équation
![]() admet donc une seule
solution dans
admet donc une seule
solution dans ![]() .
.
Avec un outil de calcul, on trouve:
![]() On en déduit
ensuite:
On en déduit
ensuite:
![]()