La démonstration (fausse)

Soit les trois points (dans une base orthonormée) $A=P_0(0)=(0,0)$, $P_0(1)=(1,1)$, $B=P_0(2)=(2,0)$.

Une simple application du théorème de Pythagore montre que $Longueur(P_0(0),P_0(1),P_0(2))=2\sqrt{2}$^1.3. On note cette longueur $\delta_0$.

Notons $P_1(1)$ le milieu de $[P_0(0),P_0(1)]$, $P_{1}(3)$ le milieu de $[P_0(1),P_0(2)]$ et $P_{1}(2)$ la projection orthogonale de $P_0(1)$ sur $[P_0(0),P_0(1)]$. Pour avoir des notations cohérentes, on pose $P_1(0)=P_0(0)$ et $P_1(4)=P_0(2)$. Cela revient en fait à ``plier'' en deux le triangle isocèle. On a toujours $\delta_1=Longueur(P_1(0),P_1(1),P_1(2),P_1(3),P_1(4))=Longueur(P_0(0),P_0(1),P_0(2))=2\sqrt{2}$ .

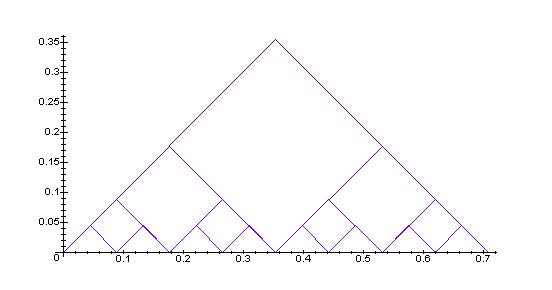
On réitère le pliage $n$ fois2is1

Plus généralement, à l'étape $n$, $n \geq 1$, pour tout entier $k$, $0 \leq k \leq 2^n$:

• si $k$ est impair, $P_n(k)$ est le milieu de $[P_{n-1}(k-1),P_{n-1}(k)]$;
• si $k$ est pair, $P_n(k)$ est la projection orthogonale de $P_{n-1}(\frac{k}{2})$ sur $[A,B]$.

et on note $\delta_n = Longueur(P_n(0),P_n(1),P_n(2),\ldots,P_n(2^n))$. Voir 1.1

Il est clair que quand $n$ tend vers l'infini, les segments formés par les points $P_n$ tendent vers le segment de droite $[A,B]$. Donc la longueur de ce segment tend vers la $Longueur(A,B)=2$. En abrégé $\lim_{n \to \infty}{\delta_n} = 2$.

D'autre part, il est évident que $\delta_n = \delta_{n-1} = \ldots = \delta{1} = \delta{0} = 2 \sqrt{2}$ .

On aboutit donc à $2\sqrt{2}=2$, soit $sqrt(2)=1$, ou encore $2=1$.