- ... prendre1.1
 représentant le logarithme en base
10
représentant le logarithme en base
10
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... libet1.2
- de quelque chose de faux, on peut trouver n'importe quoi
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
 1.3
1.3
-
 désigne
la distance (euclidienne) entre les points
désigne
la distance (euclidienne) entre les points  et
et
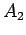 , plus la distance entre
, plus la distance entre 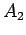 et
et  , ...plus la distance entre
, ...plus la distance entre  et
et  .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... Gardner1.4
- Traduction de logic/weighing/balance des archives de
rec.puzzles
http://alabanza.com/kabacoff/Inter-Links/puzzles.html
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... possible1.5
- je ne les écrit pas tous
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... permutations2.1
- Pour ceux qui liraient Galois, il est intéressant de
noter qu'il appelle permutation une certaine disposition de
 lettres, et emploie le terme de substitution
pour désigner l'opération de changement de cette
disposition.
lettres, et emploie le terme de substitution
pour désigner l'opération de changement de cette
disposition.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... 2.2
- Une fois que l'on a une solution
 de
l'équation en
de
l'équation en  , alors
, alors
 est solution de
l'équation en
est solution de
l'équation en  .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... suivant2.3
- si
 est solution du sytème [S],
on remarque que
est solution du sytème [S],
on remarque que
 est solution de
l'équation 3.
est solution de
l'équation 3.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...4.1
- Voir la FAQ
 .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...).4.2
- On peut définir
 de façon
plus concise:
de façon
plus concise:
 La fonction
La fonction
 est alors une surjection de
est alors une surjection de
 dans
dans  . Tout
réel
. Tout
réel
 est atteint, et
pour connaître son antécédent, il suffit
d'écrire le développement binaire de
est atteint, et
pour connaître son antécédent, il suffit
d'écrire le développement binaire de  .
En revanche,
.
En revanche,  n'est pas une bijection, en raison
de l'existence de 2 développements binaires, comme pour les
développements décimaux.
n'est pas une bijection, en raison
de l'existence de 2 développements binaires, comme pour les
développements décimaux.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ....4.3
- Tous les réels ne sont pas atteints, mais chaque
réel atteint a un antécédent unique.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...4.4
- pour une définition plus rigoureuse de
 , voir l'article de David Madore:
http://www.eleves.ens.fr:8080/home/madore/w/ordinals/ordinals.html
, voir l'article de David Madore:
http://www.eleves.ens.fr:8080/home/madore/w/ordinals/ordinals.html
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...MapleSoft 7.1
- Disponible sur les plateformes Windows, Macintosh, Linux
(min.486), DEC Alpha, HP/9000, IBM RS/6000, SGI, Sun SPARC.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... Research7.2
- Disponible sur les plateformes Windows, Macintosh, Linux, la
plupart des Unix (Sun, SGI, IBM RS/6000, HP PA-Risc, DEC AXP) et
NEXTSTEP (Motorola, x86, HP PA-RISC, SPARC), OS/2 et DEC OpenVMS
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...http://www.matlab.com7.3
- Disponible sur les plateformes Windows, Macintosh, DEC-Alpha,
HP 9000 PA-RISC, IBM RS/6000, OpenVMS, SGI, SUN, Linux (min. 486).
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...http://www.mupad.de7.4
- (versions compilées supportées disponibles pour
Windows, Linux/i486, Macintosh PPC et Sparc sous SunOS/Solaris, et
nombreuses versions non supportées).
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...ftp://ftp.inria.fr/INRIA/Projects/Meta2/Scilab
7.5
- (sources, versions compilées pour stations Unix, PC
Linux et W95, docs, help, toolboxes incluses)
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...http://halse.mathematik.tu-muenchen.de/ntsw/pari/
7.6
- (sources complètes disponibles et binaires de GP
disponibles pour Unix, Amiga, Macintosh et MS-DOS)
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...7.7
- à ce stade la représentation flottante est
utilisée donc il suffit de calculer le logarithme de la
mantisse et d'ajouter l'exposant que multiplie
 .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...\space 7.8
 est la partie entière de
est la partie entière de  divise par
divise par  qu'on pourra
additionner directement à l'exposant.
qu'on pourra
additionner directement à l'exposant.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...\space 7.9
- le calcul de la tangente n'a pas de sens si

.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...7.10
- il vaut mieux ne faire cela que pour des valeurs proches de
 afin d'éviter la division.
afin d'éviter la division.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... type7.11
- L'implémentation de argtanh est presque identique pourvu
de commencer avec
 puis de remplacer
puis de remplacer
 par
par
 et
et
 par
par
 .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... a7.12
- l'implémentation de
 s'en
déduit en commençant avec
s'en
déduit en commençant avec  , en
remplaçant
, en
remplaçant
 par
par
 ,
,
 par
par
 et
et
 par
par
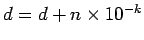 .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...7.13
- Pour sinus et cosinus: si on ajoute
 à la ligne d'initialisation ainsi que
à la ligne d'initialisation ainsi que
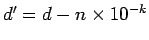 à la boucle
la plus interne et enfin
à la boucle
la plus interne et enfin
 tout à la
fin alors le sinus est donné par
tout à la
fin alors le sinus est donné par
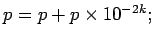 et le cosinus
par
et le cosinus
par
 (Les formules
moins efficaces
(Les formules
moins efficaces
 et
et
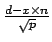 sont
plus souvent utilisées)
sont
plus souvent utilisées)
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
 de façon
plus concise:
de façon
plus concise:
 . Tout
réel
. Tout
réel
 n'est pas une bijection, en raison
de l'existence de 2 développements binaires, comme pour les
développements décimaux.
n'est pas une bijection, en raison
de l'existence de 2 développements binaires, comme pour les
développements décimaux.
