


Next: J'ai
réussi à montrer Up: Est-ce que ? Previous: Démonstration par les
séries Contents
L'argument le plus direct est de vérifier directement,
à partir de la définition de la limite, que
 est la limite pour
est la limite pour  tendant
vers l'infini de la série
tendant
vers l'infini de la série
Cela signifie qu'à condition de prendre suffisamment de
termes dans la série, on peut s'approcher d'aussi
près de  que l'on veut (c'est-à-dire
rendre la différence
que l'on veut (c'est-à-dire
rendre la différence  aussi petite que l'on veut).
aussi petite que l'on veut).
Mathématiquement, cette définition de limite
s'écrit:
 , il existe
, il existe  tel que pour tout
tel que pour tout  , on a
, on a
 .
.
En calculant
on voit facilement que si  (nombre de termes)
est suffisamment grand, alors notre somme peut s'approcher d'aussi
près que l'on veut de
(nombre de termes)
est suffisamment grand, alors notre somme peut s'approcher d'aussi
près que l'on veut de  , puisque leur
différence,
, puisque leur
différence, 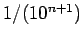 devient de plus en
plus petite quand
devient de plus en
plus petite quand  augmente.
augmente.
Pour être plus précis, si on se donne  , la différence maximale que l'on s'autorise,
alors il suffit de prendre1.1:
, la différence maximale que l'on s'autorise,
alors il suffit de prendre1.1:
Soit
 . Si
. Si
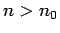 , on aura alors:
, on aura alors:
la condition est respectée, donc la limite vaut  , et
, et




Next: J'ai
réussi à montrer Up: Est-ce que ? Previous: Démonstration par les
séries Contents
Faq de fr.sci.maths 2003-12-14
![]() est la limite pour
est la limite pour ![]() tendant
vers l'infini de la série
tendant
vers l'infini de la série
![]() , il existe
, il existe ![]() tel que pour tout
tel que pour tout ![]() , on a
, on a
![]() .
.
![]() , la différence maximale que l'on s'autorise,
alors il suffit de prendre1.1:
, la différence maximale que l'on s'autorise,
alors il suffit de prendre1.1:![]() . Si
. Si
![]() , on aura alors:
, on aura alors: