(i) ![]() . L'équation s'écrit donc
. L'équation s'écrit donc
![]() Cette équation a trois
solutions dans
Cette équation a trois
solutions dans ![]() :
:
![]() ,
, ![]() et
et
![]() . Où
. Où
![]()
(ii) ![]() . L'équation est
. L'équation est
![]() . On effectue un autre
changement de variable z = u + v. Avec u non-nul. Et
l'équation s'écrit:
. On effectue un autre
changement de variable z = u + v. Avec u non-nul. Et
l'équation s'écrit:
![]() on
s'intéresse alors au système suivant2.3:
on
s'intéresse alors au système suivant2.3:
Le système [S] est équivalent à:
Encore (!) un changement de variable dans la première
équation. On pose 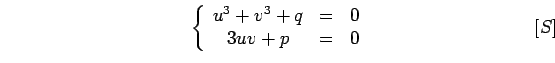 , et celle-ci
devient:
, et celle-ci
devient:
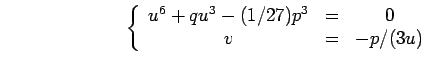 . De là, une
solution est donc:
. De là, une
solution est donc:
![]()
Donc, il ne reste plus qu'à trouver les solutions de
![]() . C'est le cas (i). On a donc comme
solutions:
. C'est le cas (i). On a donc comme
solutions:
De là, on a
![]() ,
,
 et
et
![]() . Ce qui nous donne les
solutions pour
. Ce qui nous donne les
solutions pour ![]() ...
...