


Next: Démonstrations Up: La suite , , Previous:
La suite , ,
Contents
C'est vrai pour  . Soit
. Soit 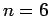 ,
supposons la propriété vérifiée pour
,
supposons la propriété vérifiée pour
 et montrons la pour
et montrons la pour  . Si
. Si
 est pair,
est pair,  se termine par
se termine par
 . Le chiffre précédent,
s'il existe, n'est pas un
. Le chiffre précédent,
s'il existe, n'est pas un  (puisqu'on n'a pas 4
chiffres identiques consécutifs).
(puisqu'on n'a pas 4
chiffres identiques consécutifs).
Donc  se termine par un bloc de trois 2, puis
un bloc de deux 1, puis un 2, et donc
se termine par un bloc de trois 2, puis
un bloc de deux 1, puis un 2, et donc  se
termine par
se
termine par  ;
;  étant impair, c'est précisément ce qu'on
attendait.
étant impair, c'est précisément ce qu'on
attendait.
Si  est impair,
est impair,  se termine
par
se termine
par  . Peu importe si le chiffre
précédent est un 3 ou non, seuls les trois derniers
blocs nous intéressent, et
. Peu importe si le chiffre
précédent est un 3 ou non, seuls les trois derniers
blocs nous intéressent, et  se
termine donc par
se
termine donc par  ;
;  étant pair, c'est ce qu'on attendait.
étant pair, c'est ce qu'on attendait.
![\begin{lemme}[2] Soit $x_n$\ la suite définie pour $n\ge6$\ par $x_6=222112$, $x... ...ge10$, $x_{n+1}$\ est égal à $D(x_n)$\ privé de son premier chiffre. \end{lemme}](img278.png)
- Pour tout
 ,
,  est un
suffixe de
est un
suffixe de  .
.
- Pour tout
 ,
,  est un
suffixe de
est un
suffixe de  .
.
- Pour
 ,
,  est
impair et
est
impair et
 .
.
- Pour tout
 ,
,  .
.
Faq de fr.sci.maths 2003-12-14
![]() se termine par un bloc de trois 2, puis
un bloc de deux 1, puis un 2, et donc
se termine par un bloc de trois 2, puis
un bloc de deux 1, puis un 2, et donc ![]() se
termine par
se
termine par ![]() ;
; ![]() étant impair, c'est précisément ce qu'on
attendait.
étant impair, c'est précisément ce qu'on
attendait.![]() est impair,
est impair, ![]() se termine
par
se termine
par ![]() . Peu importe si le chiffre
précédent est un 3 ou non, seuls les trois derniers
blocs nous intéressent, et
. Peu importe si le chiffre
précédent est un 3 ou non, seuls les trois derniers
blocs nous intéressent, et ![]() se
termine donc par
se
termine donc par ![]() ;
; ![]() étant pair, c'est ce qu'on attendait.
étant pair, c'est ce qu'on attendait.![]()
 ,
,  ,
,