Démonstrations

1. Par récurrence sur $n$, d'après la définition de $u_n$. Noter qu'il est important d'enlever le premier chiffre de $D(x_n)$ pour construire $x_{n+1}$, car le chiffre précédant $x_n$ dans $u_n$ peut être identique au premier chiffre de $x_n$, ce qui modifie la longueur du premier bloc; en revanche, le second chiffre de $D(x_n)$, qui indique la nature du premier bloc de $x_n$, peut être conservé car il apparaît bien à cet endroit dans $u_{n+1}$. Au passage, on peut noter que ce chiffre est toujours un 2.

2. Par récurrence sur $n$. On le vérifie à la main pour $n<10$. Pour $n\ge10$, si $x_n$ est un suffixe de $x_{n+2}$, alors $x_{n+1}$ est un suffixe strict de $D(x_{n+2})$, donc c'est un suffixe de $x_{n+3}$.

3. Pour $n\ge11$, la longueur de $x_n$ est impaire par construction. On montre $\vert x_{n+2}\vert \ge \vert x_n\vert+2$ par récurrence. C'est vrai pour $n=11$ (et même $n=9$ et $n=10$). Supposons que $\vert x_{n+2}\vert \ge \vert x_n\vert+2$ pour un certain $n\ge11$. Comme $x_n$ est un suffixe de $x_{n+2}$, on peut écrire $x_{n+2} = w x_n$, avec $\vert w\vert \ge 2$.

L'avant dernier chiffre de $w$ ne peut être égal au premier chiffre de $x_n$, car il s'agit de deux chiffres consécutifs en position impaire qui sont toujours distincts dans une image par $D$.

Par conséquent $D(x_{n+2})$ contient au moins un bloc de plus que $D(x_n)$ et donc $\vert D(x_{n+2})\vert \ge \vert D(x_n)\vert+2$, d'où $\vert x(n+3)\vert \ge \vert x_{n+1}\vert+2$.

4. Se déduit facilement des valeurs initiales et de (3).

C'est vrai d'après le lemme 1 pour 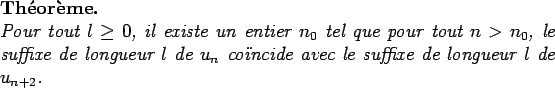$l \leq 6$, en prenant $n_0 = 6$. Pour $l$ supérieur à $6$, on prend $n_0 = l+2$. Alors pour $n > n_0$, le suffixe de longueur $l$ de $u_n$ est un suffixe de $x_n$, puisque $\vert x_n\vert \geq n-2 \geq l$ d'après le 4. du lemme 2.

Il coïncide donc avec le suffixe de longueur $l$ de $u_{n+2}$, puisque $x_n$ est un suffixe de $x_{n+2}$ qui est un suffixe de $u_{n+2}$. (d'après les 2. et 1. du lemme 2. )

On peut formaliser ce résultat en définissant une topologie convenable sur l'ensemble des mots finis et infinis sur l'alphabet $\{1,2,3\}$. On peut alors montrer que la suite $u_n$ a deux valeurs d'adhérence, qui sont deux mots infinis à gauche: $$\begin{split} &\ldots131221121321131112111322311211132132212... ...113121322111213112221133211322112211213322\ &112 \end{split}$$