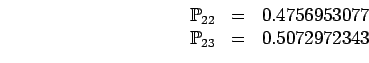 avec une
machine à calculer, on obtient un dépassement de
capacité. Il faut donc réfléchir un peu pour
faire le calcul, en tenant compte des possibilités
informatiques.
avec une
machine à calculer, on obtient un dépassement de
capacité. Il faut donc réfléchir un peu pour
faire le calcul, en tenant compte des possibilités
informatiques.
Si on dispose d'un logiciel de calcul mathématique, tel que Maple ou Mathématica, le problème de dépassement de capacité disparaît, et on utilise n'importe laquelle des expressions ci-dessus.
Si on dispose d'une calculatrice programmable, il est possible de programmer, avec une boucle, le calcul de l'expression:
Si l'on dispose d'un tableur, l'expression:
 est
facile à calculer en faisant un tableau de taille
est
facile à calculer en faisant un tableau de taille
![]() , avec
, avec ![]() colonnes: une
colonne pour
colonnes: une
colonne pour ![]() , une colonne pour
, une colonne pour
![]() , une colonne pour le
produit.
, une colonne pour le
produit.
Si l'on n'a qu'une calculatrice scientifique, il est nécessaire d'utiliser une approximation. Il faut remarquer que
Or, si ![]() est beaucoup plus petit que
est beaucoup plus petit que ![]() , on a:
, on a:
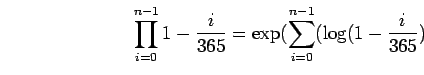 .
Et comme la somme des
.
Et comme la somme des ![]() premiers entiers est
égal à
premiers entiers est
égal à
![]() .
.
On a donc:
Cette approximation est relativement précise. Elle donne
les valeurs suivantes pour 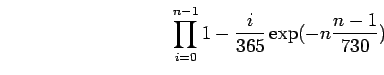 et
et
![]() , ce qui donne une réponse
juste pour la question (2) malgré la très forte
proximité de
, ce qui donne une réponse
juste pour la question (2) malgré la très forte
proximité de ![]() avec
avec ![]() :
: